Динамическая задача

                Если нагрузки на систему меняются во времени, т.е. f = f(t), то следует полагать функциями времени также усилия и перемещения, что может потребовать введения в рассмотрение скоростей dZ/dt и ускорений d2Z/dt2 . Когда возникающие при этом силы инерции

                                                                          J(t) = M(d2Z/dt2)                                                                                            (19.11)

не могут считаться пренебрежимо малыми по сравнению с нагрузками на систему и с силами упругости, то их следует учесть при формировании условий равновесия, которые примут вид дифференциальных уравнений

                                                                  M(d2Z/dt2) + KZ(t) = f(t).                                                                                    (19.12)

                Если все массы сосредоточены в узлах системы, то матрица масс М будет диагональной, в остальных же случаях приведение ее к диагональному виду представляет собой приближенный подход (он применен при разработке комплекса).

Задача определения характеристик собственных колебаний системы (модальный анализ) заключается в нахождении условий, при которых ненагруженная система совершает гармонические колебания по закону

                                                                       Z(t) = Ysin(wt + j).                                                                                         (19.13)

В выражении (19.13) вектор Y характеризует форму собственных колебаний (соотношения между смещениями узлов), w – их частоту, j – начальную фазу. Подстановка (19.13) в (19.12) с учетом того, что f(t) = 0 дает уравнение для собственных колебаний

                                                                          (K - w2M) Y= 0,                                                                                            (19.14)

нетривиальное решение которого существует лишь тогда, когда величины wi (i = 1,...,n), называемые собственными частотами, обращают в нуль детерминант матрицы (K - w2M). Соответствующие им формы собственных колебаний Yi

ўлзЁб«повбп «Ёим б в®з­®бвмо ¤® Їа®Ё§ў®«м­®Ј® ¬­®¦ЁвҐ«п. ќв®в ¬­®¦ЁвҐ«м ­ §­ зҐ­ в ЄЁ¬ ®Ўа §®¬, зв® ¬ ЄбЁ¬ «м­ п Є®¬Ї®­Ґ­в  ўҐЄв®а  Yi а ў­  Ґ¤Ё­ЁжҐ. ‘«Ґ¤гҐв в Є¦Ґ ®в¬ҐвЁвм бў®©бвў® ®ав®Ј®­ «м­®бвЁ б®Ўб⢥­­ле ўҐЄв®а®ў Є Є ®в­®бЁвҐ«м­® ¬ ваЁжл ¬ бб, в Є Ё ®в­®бЁвҐ«м­® ¬ ваЁжл ¦ҐбвЄ®бвЁ, в.Ґ.

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя YiÒMYj= 0яя яèяяя YiÒKYj= 0яяяяя ïðè i ¹ j.яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.15)

яяяяяяяяяяяяяяя ЏаЁ ¤Ё­ ¬ЁзҐбЄ®¬ а бзҐвҐ зЁб«® Є®¬Ї®­Ґ­в ўҐЄв®а  Z, б Є®в®ал¬Ё бўп§ ­л Ё­ҐажЁ®­­лҐ бЁ«л (Є®«ЁзҐбвў® ¤Ё­ ¬ЁзҐбЄЁе б⥯Ґ­Ґ© бў®Ў®¤л), § з бвго Ўлў Ґв ­ ¬­®Ј® ¬Ґ­миЁ¬, 祬 ЇаЁ бв вЁзҐбЄ®¬ а бзҐвҐ. ’ЁЇЁз­л¬ ЇаЁ¬Ґа®¬ ¬®Јгв б«г¦Ёвм Ї®ў®а®вл 㧫®ў, ®Ўлз­® ®Є §лў ойЁҐ §­ зЁвҐ«м­® ¬Ґ­м襥 ¤Ё­ ¬ЁзҐбЄ®Ґ ў«Ёп­ЁҐ, 祬 Ёе «Ё­Ґ©­лҐ ᬥ饭Ёп. ‚ SCAD Ё­ҐажЁ®­­лҐ ¬®¬Ґ­вл, ᮮ⢥вбвўгойЁҐ Ї®ў®а®в ¬ 㧫®ў Ё ¤агЈЁҐ Ё­ҐажЁ®­­лҐ е а ЄвҐаЁбвЁЄЁ ¬®Јгв Ўлвм Їа®ЁЈ­®аЁа®ў ­л, ®¤­ Є® н⮠㦥 § ¤ Ґв б ¬ Ї®«м§®ў вҐ«м, д®а¬г«Ёагп § ¤ зг ¤Ё­ ¬ЁзҐбЄ®Ј® а бзҐв . …б«Ё з бвм Ё­ҐажЁ®­­ле б®бв ў«пойЁе ­ Јаг§ЄЁ ­Ґ гзЁвлў Ґвбп, в® а §¤Ґ«пп ўҐЄв®а Y ­  Ї®¤ўҐЄв®а YO, ¤«п Є®в®а®Ј® бЁ«л Ё­ҐажЁЁ а ў­л ­г«о, Ё Ї®¤ўҐЄв®а YI, бўп§ ­­л© б Ё­ҐажЁ®­­л¬Ё бЁ« ¬Ё, ¬®¦­® § ЇЁб вм бЁб⥬г (19.14) ў д®а¬Ґ

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя KOO YO + KOI YIя = 0;

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя KIO YOя + KII YIя = w2MII .яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.16)

€§ нв®© бЁбвҐ¬л ЁбЄ«оз Ґвбп Ї®¤ўҐЄв®а YO Ё ў १г«мв вҐ гЄ § ­­®© Їа®жҐ¤гал "бв вЁзҐбЄ®Ј® гЇ«®в­Ґ­Ёп" а §¬Ґа­®бвм § ¤ зЁ ¬®¤ «м­®Ј®  ­ «Ё§  १Є® 㬥­ми Ґвбп Ё ®­  ЇаЁ®ЎаҐв Ґв ўЁ¤

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (KOO-1 MIIя - l2 I) YIя = 0,яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.17)

Ј¤Ґ I - Ґ¤Ё­Ёз­ п ¬ ваЁж ,   l = 1/w.



‚ Є зҐб⢥ १г«мв в®ў ¬®¤ «м­®Ј®  ­ «Ё§  SCAD ўл¤ Ґв б®Ўб⢥­­лҐ зЁб«  li Ё б®Ўб⢥­­лҐ ўҐЄв®ал YI § ¤ зЁ (19.17). ‘ ­Ё¬Ё бўп§ ­л ЄагЈ®ў п з бв®в  w = 1/l (а ¤/ᥪ), жЁЄ«ЁзҐбЄ п з бв®в  q = w/2p (ЈҐаж) Ё ЇҐаЁ®¤ ’ = 1/q.

‚ бЁ«г ®ав®Ј®­ «м­®бвЁ д®а¬ б®Ўб⢥­­ле Є®«ҐЎ ­Ё© аҐиҐ­ЁҐ «оЎ®© ¤Ё­ ¬ЁзҐбЄ®© § ¤ зЁ ў ўЁ¤Ґ а §«®¦Ґ­Ёп

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя Z(t) = (t)Yiяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.18)

ўҐ¤Ґв Є а бЇ ¤г бЁбвҐ¬л ¤ЁддҐаҐ­жЁ «м­ле га ў­Ґ­Ё© (19.12) ­  ­Ґ§ ўЁбЁ¬лҐ ®в­®бЁвҐ«м­® ®Ў®ЎйҐ­­ле Є®®а¤Ё­ в yi(t). ќвЁ га ў­Ґ­Ёп б гзҐв®¬ Їа®Ї®ажЁ®­ «м­®Ј® бЄ®а®бвЁ ¤®Ї®«­ЁвҐ«м­®Ј® з«Ґ­ , б Ї®¬®ймо Є®в®а®Ј® гзЁвлў Ґвбп б®Їа®вЁў«Ґ­ЁҐ ¤ўЁ¦Ґ­Ёо, Ё¬Ґов ўЁ¤

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя d2 yi /dt2 + 2xi dyi /dt +wi2 yi я= Pi(t)/Mi.яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.19)

ЋЎ®ЎйҐ­­лҐ бЁ«л

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя Pi(t) = w2 YTi f(t),яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.20)

¬ ббл

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя Mi =MYiяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.21)

Ё Ї а ¬Ґвал § вге ­Ёп xi , б®ў¬Ґбв­® б ­ з «м­л¬Ё гб«®ўЁп¬Ёя yoi Ё y1i , Ї®«гз Ґ¬л¬Ё Ё§ Zo = Z(0) Ё

Z1 = dZ(0)/dt Ї® д®а¬г« ¬

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя yoi = MZo ,яя y1i = MZ1яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.22)

Ї®«­®бвмо ®ЇаҐ¤Ґ«пов аҐиҐ­ЁҐ § ¤ зЁ. ќв® аҐиҐ­ЁҐ ¤ Ґвбп ўла ¦Ґ­ЁҐ¬

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя yi = exp[-xi wi t] {[(yoi xi wi + y1i)/ wDi] sinwDitя +я yoi} +яя

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя + (1/wDiMi) exp[-xi wi (t - t)] sinwDi(t - t)dt ,яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.23)



ў Є®в®а®¬ ЇҐаў®Ґ б« Ј Ґ¬®Ґ гзЁвлў Ґв ­ з «м­лҐ гб«®ўЁп,   ўв®а®Ґ ­®бЁв ­ §ў ­ЁҐ Ё­вҐЈа «  „о ¬Ґ«п.

‚室пй п ў ўла ¦Ґ­ЁҐ (19.23) з бв®в  ¤Ґ¬ЇдЁа®ў ­­ле Є®«ҐЎ ­Ё©

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя wDi = wi (1 - xI2)1/2яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.24)

¬ «® ®в«Ёз Ґвбп ®в wi ЇаЁ ®Ўлз­ле §­ зҐ­Ёпе «®Ј аЁд¬ЁзҐбЄ®Ј® ¤ҐЄаҐ¬Ґ­в 

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя d = 2pxw/wD > 2px.яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.25)

19.3. ђҐиҐ­ЁҐ бЁб⥬ га ў­Ґ­Ё©

яяяяяяяяяяяяяяя Џ®б«Ґ в®Ј®, Є Є § ¤ ­­ п Є®­бвагЄжЁп ЇаҐ¤бв ў«Ґ­  ў ўЁ¤Ґ Є®­Ґз­®н«Ґ¬Ґ­в­®© бвагЄвгал, § ¤ з  ®Ў ®ЇаҐ¤Ґ«Ґ­ЁЁ ЇҐаҐ¬ҐйҐ­Ё© 㧫®ў бў®¤Ёвбп Є аҐиҐ­Ёо бЁбвҐ¬л «Ё­Ґ©­ле  «ЈҐЎа ЁзҐбЄЁе га ў­Ґ­Ё© ўЁ¤ 

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя KZ=F,яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.26)

Ј¤Ґ: K - бЁ¬¬ҐваЁз­ п Ї®«®¦ЁвҐ«м­® ®ЇаҐ¤Ґ«Ґ­­ п ¬ ваЁж  а §¬Ґа®¬ N´N; F - ¬ ваЁж  Їа ўле з б⥩ (§ Ја㦥­Ё©) а §¬Ґа®¬ N´k (k - Є®«ЁзҐбвў® § Ја㦥­Ё©); Z - ЁбЄ®¬ п ¬ ваЁж  ЇҐаҐ¬ҐйҐ­Ё© а §¬Ґа®¬ k´N.

яяяяяяяяяяяяяяя Џ®бЄ®«мЄг ў Ў®«миЁ­б⢥ б«гз Ґў ¬ ваЁж  K пў«пҐвбп ࠧ०Ґ­­®©, в® ¤«п 㬥­м襭Ёп вॡ㥬®© ®ЇҐа вЁў­®© Ї ¬пвЁ, ў­Ґи­Ґ© Ї ¬пвЁ Ё ўаҐ¬Ґ­Ё бзҐв  ЇаҐ¤ў аЁвҐ«м­® Їа®Ё§ў®¤Ёвбп ЇҐаҐ­г¬Ґа жЁп ­ҐЁ§ўҐбв­ле бЁб⥬л (19.26) б 楫мо ¬Ё­Ё¬Ё§ жЁЁ Їа®дЁ«п ¬ ваЁжл (аЁб.19.2).



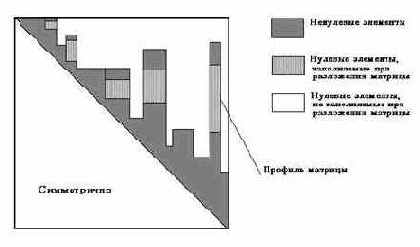
ђЁб.19.2

яяяяяяяяяяяяяяя

‚ Є®¬Ї«ҐЄбҐ SCAD ॠ«Ё§®ў ­® ­ҐбЄ®«мЄ® ¬Ґв®¤®ў ЇҐаҐ­г¬Ґа жЁЁ,   Ё¬Ґ­­®, ®Ўа в­л©  «Ј®аЁв¬ Љ веЁ«« -Њ ЄЄЁ, ¬Ґв®¤-д Єв®а ¤ҐаҐўмҐў, ¬Ґв®¤ ў«®¦Ґ­­лx бҐзҐ­Ё© Ё  «Ј®аЁв¬ Ї а ««Ґ«м­ле бҐзҐ­Ё©. ЋЇЁб ­ЁҐ нвЁе ¬Ґв®¤®ў Ё Ёе ба ў­ЁвҐ«м­ п е а ЄвҐаЁбвЁЄ  ЇаЁўҐ¤Ґ­л ў бЇҐжЁ «м­®© «ЁвҐа вгаҐ. Џ®«м§®ў вҐ«о ЇаҐ¤®бв ў«Ґ­  ў®§¬®¦­®бвм ўлЎ®а  ¬Ґв®¤  ЇҐаҐ­г¬Ґа жЁЁ. Џ® 㬮«з ­Ёо ЁбЇ®«м§гҐвбп ®Ўа в­л©  «Ј®аЁв¬ Љ веЁ«« -Њ ЄЄЁ, в.Є. г нв®Ј® ¬Ґв®¤  ¬Ё­Ё¬ «м­лҐ § Їа®бл Є ®ЇҐа вЁў­®© Ї ¬пвЁ. Њл ­Ґ ¬®¦Ґ¬ ¤ вм Є®­ЄаҐв­лҐ ४®¬Ґ­¤ жЁЁ ¤«п ўлЎ®а  ¬Ґв®¤  ЇҐаҐ­г¬Ґа жЁЁ, в.Є. нд䥪⨢­®бвм в®Ј® Ё«Ё Ё­®Ј®  «Ј®аЁв¬  §­ зЁвҐ«м­® § ўЁбЁв ®в бвагЄвгал Є®­ЄаҐв­®© ¬ ваЁжл Љ.



яяяяяяяяяяяяяяя „«п аҐиҐ­Ёп бЁб⥬л (19.26) ЇаҐ¤ў аЁвҐ«м­® Їа®Ё§ў®¤Ёвбп ваҐгЈ®«м­®Ґ а §«®¦Ґ­ЁҐ ¬ ваЁжл Љ ¬®¤ЁдЁжЁа®ў ­­л¬ ¬Ґв®¤®¬ ѓ гбб  б ўлЎ®а®¬ а §аҐи о饣® н«Ґ¬Ґ­в  ­  Ј« ў­®© ¤Ё Ј®­ «Ё ў Ї®ап¤ЄҐ б«Ґ¤®ў ­Ёп ЇҐаҐ­г¬Ґа®ў ­­ле ­ҐЁ§ўҐбв­ле.

яяяяяяяяяяяяяяя …б«Ё ў Їа®жҐбᥠваҐгЈ®«м­®Ј® а §«®¦Ґ­Ёп ¬ ваЁжл K ®¤Ё­ Ё§ а §аҐи ойЁе н«Ґ¬Ґ­в®ў ®Є ¦Ґвбп а ў­л¬ ­г«о, в.Ґ. ўлпб­Ёвбп, зв® K - ўл஦¤Ґ­ , зв® бўЁ¤ҐвҐ«мбвўгҐв ® ЈҐ®¬ҐваЁзҐбЄ®© Ё§¬Ґ­пҐ¬®бвЁ бЁб⥬л, в® Їа®Ё§ў®¤Ёвбп  ўв®¬ вЁзҐбЄ®Ґ ­ «®¦Ґ­ЁҐ ¤®Ї®«­ЁвҐ«м­®© ­Ґ­ Їа殮­­®© бўп§Ё, ЇаҐўа й о饩 бЁб⥬㠢 ­ҐЁ§¬Ґ­пҐ¬го. ЏаЁ н⮬ Ї®«м§®ў вҐ«о ЇаҐ¤®бв ў«пҐвбп Ё­д®а¬ жЁп ® ­®¬Ґа е 㧫®ў Ё вЁЇ е б⥯Ґ­Ґ© бў®Ў®¤л, Ї® Є®в®ал¬ Їа®Ё§ўҐ¤Ґ­® ­ «®¦Ґ­ЁҐ бўп§Ґ©. ‡ ¬ҐвЁ¬, зв® ўл஦¤Ґ­ЁҐ Ё¤Ґ­вЁдЁжЁагҐвбп ­Ґ Ї® в®з­®¬г а ўҐ­бвўг а §аҐи о饣® н«Ґ¬Ґ­в  ­г«о,   Ї® Ї®пў«Ґ­Ёо ­  Ј« ў­®© ¤Ё Ј®­ «Ё зЁб«  "Їа ЄвЁзҐбЄЁ а ў­®Ј® ­г«о" Ё ўлЎ®а нв®Ј® Ї®а®Ј  (Ї а ¬Ґва в®з­®бвЁ аҐиҐ­Ёп) пў«пҐвбп ®¤­Ё¬ Ё§ Ї а ¬Ґва®ў, Є®в®ал¬ Ї®«м§®ў вҐ«м ¬®¦Ґв а бЇ®ап¤Ёвмбп б ¬.

яяяяяяяяяяяяяяя Љ®Ј¤  б®®ЎйҐ­Ёп ®Ў гбв ­®ўЄҐ ¤®Ї®«­ЁвҐ«м­ле бўп§Ґ© Ї®пў«повбп ў Їа®в®Є®«Ґ аҐиҐ­Ёп § ¤ зЁ, ¬л ४®¬Ґ­¤гҐ¬ ў­Ё¬ вҐ«м­® Їа® ­ «Ё§Ёа®ў вм а бзҐв­го б奬㠨 ўлпб­Ёвм ЇаЁзЁ­г Їа®Ёб宦¤Ґ­Ёп ЈҐ®¬ҐваЁзҐбЄ®© Ё§¬Ґ­пҐ¬®бвЁ Є®­бвагЄжЁЁ. ‚®§¬®¦­® ¤«п  ­ «Ё§  Ї®­ ¤®ЎЁвбп аҐиЁвм § ¤ зг б­®ў  б ¤агЈЁ¬ §­ зҐ­ЁҐ¬ Ї а ¬Ґва  в®з­®бвЁ аҐиҐ­Ёп.

яяяяяяяяяяяяяяя „®Ї®«­ЁвҐ«м­л¬ бҐаўЁб­л¬ б।бвў®¬ пў«пҐвбп Є®­ва®«м аҐиҐ­Ёп бЁб⥬л (19.26). ЏаЁ Ї®пў«Ґ­ЁЁ б®®ЎйҐ­Ёп ® Ў®«ми®© ўҐ«ЁзЁ­Ґ ®иЁЎЄЁ аҐиҐ­Ёп, Є®в®а®Ґ, Є Є Їа ўЁ«®, пў«пҐвбп б«Ґ¤бвўЁҐ¬ Ї«®е®© ®Ўгб«®ў«Ґ­­®бвЁ ¬ ваЁжл K, б«Ґ¤гҐв ў­Ё¬ вҐ«м­® Їа® ­ «Ё§Ёа®ў вм ЇҐаҐ¬ҐйҐ­Ёп 㧫®ў Ё гЎҐ¤Ёвмбп ў ⮬, зв® Ї®«г祭­®Ґ аҐиҐ­ЁҐ пў«пҐвбп ЇаЁҐ¬«Ґ¬л¬ б Ё­¦Ґ­Ґа­®© в®зЄЁ §аҐ­Ёп. Џ«®е п ®Ўгб«®ў«Ґ­­®бвм з йҐ ўбҐЈ® бўп§ ­  б ­Ґг¤ з­®© Є®­бвагЄжЁҐ© а ббзЁвлў Ґ¬®© бЁб⥬л (­ ЇаЁ¬Ґа, б«гз © "Ї®звЁ Ё§¬Ґ­пҐ¬®©" бЁб⥬л) Ё«Ё ҐҐ ­Ґг¤ з­®© Ё¤Ґ «Ё§ жЁҐ©.


Содержание раздела

---

---