Спектры ответа

14.1 Расчет на сейсмические воздействия

Выведенный из положения равновесия линейный неконсервативный осциллятор совершает затухающие колебания, которые описываются дифференциальным уравнением

                                                                 (14.1)

где

                w – собственная круговая частота системы без затухания (рад/с);

                j – относительное демпфирование. При j < 1 решение уравнения (1) имеет вид

где

               

 – частота с учетом затухания,

                А, a – коэффициенты, которые зависят от начальных условий.

                Обычно для строительных конструкций j<<1 и практически

.

                Если на массу действует сила F(t), то ее перемещения описываются уравнением

                                                   (14.2)

общее решение которого при нулевых начальных условиях можно записать с помощью интеграла Дюамeля

                  (14.3)

                При движении основания с ускорением

 (кинематическое возмущение) на массу m действует переносная сила инерции . Поэтому уравнение, описывающее относительные перемещения массы в системе координат, связанной с основанием, имеет вид

,                                                        (14.4)

а его решение

                               (14.5)

                При определении абсолютного ускорения массы

 получаем при обычных малых значениях j, что

(14.6)

                Нами рассматриваются колебания линейных дискретных систем со многими степенями свободы, полученные из любых континуальных или комбинированных систем после применения к ним процедуры дискретизации метода конечных элементов (МКЭ). При этом решается система обыкновенных дифференциальных уравнений

                                                                 (14.7)

где          {u} – вектор перемещений;

                [M] – матрица массы;

                [K] – матрица жесткости.

Вынужденные колебания линейной дискретной системы с затуханием по гипотезе Фойгта-Кельвина описываются системой обыкновенных дифференциальных уравнений

,                                            (14.8)

где          [C] – матрица диссипации энергии;

                {F(t)} – вектор нагрузки.

                В случае кинематического возмущения в качестве нагрузки выступают переносные силы инерции и система уравнений (14.8) записывается в виде

,                               (14.9)

где          {u} – вектор относительных перемещений (например, в системе координат xOy, связанной с основанием);

                {I} – вектор, компонентами которого являются косинусы углов между направлениями перемещений по координатам и вектором ускорения основания;

                - ускорение основания.

                Решение уравнения (14.9) отыскивается в виде разложения его по формам собственных колебаний системы (так называемая “модальная суперпозиция”)

,                                                                    (14.10)

где          n – число степеней свободы системы (учитываемых собственных чисел и векторов);

                 – j-я форма собственных свободных колебаний дискретной системы;

                 – неизвестные функции времени, которые необходимо определить.

                Будем предполагать, что для матрицы диссипации [С] выполняется условие



где wi – i-я собственная частота дискретной системы.

                После подстановки (14.10) в (14.9) и умножения (14.9) на вектор  для нахождения  получаем дифференциальное уравнение

,                                   (14.11)

где         

                Для определения инерционных нагрузок на конструкцию необходимо знать абсолютные ускорения ее точек:



             Сейсмические колебания дискретных систем описываются системами дифференциальных уравнений (8) с несколько более общим видом правой части:

,     (14.12)

где          и  – компоненты расчетной акселерограммы. Если какая-либо из компонент не учитывается, то соответствующая часть нагрузки из (14.12) исключается.

14.2 Поэтажные акселерограммы и спектры ответа

При анализе сейсмостойкости оборудования необ­ходимо определить действующие на него инерционные сейс­мические нагрузки. Принят метод раз­дель­ного рассмотрения сейсмических колебаний здания и обо­ру­дования с использованием так называемых поэтажных аксе­лерограмм и поэтажных спектров ускорений – акселе­рограмм и спектров, рассчитанных для точек крепления оборудования.



                Расчет производится следующим образом:

• определяются (вычисляются) вынужденные коле­ба­ния сооружения при сейсмическом воздейст­вии, заданном расчетной акселерограммой на грунте;



• определяются законы изменения абсолютных ускорений выбранных точек конструкции;



• принимая акселерограммы в качестве возмущающего воздействия, рассчитывают вы­нуж­ден­ные линейные колебания линейных некон­сер­вативных осцилляторов, и находят зависимость модулей их максимальных абсолютных уско­рений от их собственных частот и коэффициентов диссипации.


Таким образом, для каждой исследуемой точки решается уравнение (2), в котором:


• зафиксирован коэффициент диссипации j;



• нагрузкой является вычисленное возмущающее воздействие от расчетной акселерограммы;


наборы собственных частот осциляторов при расчете спектра ответа зафиксированы и приведены в таблице 14.1.

Таблица 14.1.



Частотный диапазон (гц)	Приращения (гц)
0.2 – 3.0 3.0 – 3.6 3.6 – 5.0 5.0 – 8.0 8.0 – 15.0 15.0 – 18.0 18.0 – 22.0 22.0 – 34.0	0.10 0.15 0.20 0.25 0.5 1.0 2.0 3.0

К приведенным в табл. 14.1 значениям частот неконсервативных осцилляторов добавляются еще собственные частоты рассчитываемой конструкции. Это делается для того, чтобы учесть возможность резонанса с ними.

                Для каждого указанного осцилятора находятся решения на всем диапазоне действия акселерограммы и выбирается максимальное по абсолютной величине, которое и является спектром ответа данной точки на действие данной акселерограммы.

14.3 Ввод данных и анализ результатов

Окно постпроцессора Спектры ответа (рис. 14.3.1) содержит список с номерами узлов, для которых необходимо вычислить спектры ответа (Список узлов). Имена акселерограмм, по которым необходимо выполнить расчет спектров, выбираются из списка имеющихся (Исходные) и переносятся в список используемых в расчете (Выбранные) с помощью кнопки Добавить. Если случайно выбрана не та акселерограмма, то ее можно убрать из списка Выбранные



кнопкой Вернуть. Кроме того для расчета необходимо установить направление действия, ввести коэффициент диссипации (в диапазоне от 0 до 1) и, если это необходимо, задать коэффициенты диссипации по формам (например, для

4-х форм следует ввести через пробел четыре числа). Если введено меньше значений, чем задано форм, то последнее введенное значение будет отнесено ко всем последующим формам.

                Выбор загружений, для которых выполняется расчет, осуществляется в списке, размещенном в нижней части экрана.

                Расчет выполняется после подготовки всех данных нажатием кнопки ОК. После окончания расчета открывается доступ к кнопке Результаты.

                Просмотр результатов и их документирование выполняется в диалоговом окне Результаты. Для построения спектров необходимо назначить номер узла, номер загружения и имя акселерограммы. Программа позволяет получить на одном графике спектры по одному или нескольким направлениям, во всем диапазоне частот или в заданном. Полученные графики и результаты расчета могут быть выведены на принтер кнопками Печать графиков и Результаты (таблицы) соответственно.





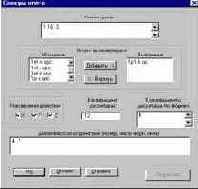
Рис. 14.3.1. Диалоговое окно

          Спектры ответа





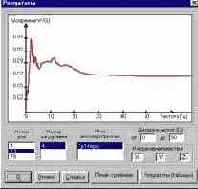
Рис. 14.3.2. Диалоговое окно Результаты

 

 

 

 

 

 

 

 

14.4 Подготовка файлов акселерограмм

Файлы акселерограмм находятся в корневом каталоге ПВК SCAD и имеют расширение SPC. При передаче пользователям постпроцессора поставляются для примера четыре стандартные акселерограммы.

                Рассмотрим пример задания акселерограммы:

Расчетная акселерограмма в cм/(c*c) для ПЗ  на площадке атомного реактора.

Компонента  –  SH.  Mодель – 1c.  Amax =  45.1 cм/(c*c).

Количество точек N =  2047; Шаг по времени Dt =  0.05000 c.

                #

                0.01 2047 0.05

0.0     0.0     0.1     0.3     0.4     0.6     0.5     0.0    –2.1    –2.6 …

               

После символа # следуют:


• коэффициент перевода заданных ускорений в м/ceк2 ;



• количество точек;



• шаг по времени;



• значения ускорений.


                Аналогичным образом может быть подготовлен файл с нужной акселерограммой (файл с расширением SPC следует поместить в каталог с исходными данными). Для использования акселе­рограмм, поставляемых в составе комплекса, соответствующие файлы необходимо скопировать из каталога SCAD в каталог с исходными данными.


Содержание раздела



---







---