Водонасыщенные грунты
Во многих случаях, в особенности при рассмотрении гидроэнергетических сооружений, следует считаться с тем, что грунты основания являются водонасыщенными. Теория таких сред, развитая Био [22], в которой учитывается упругое и вязкое взаимодействие твердой и жидкой фаз в пористоупругой насыщенной жидкостью двухфазной среде, достаточно сложна и используется чаще всего при решении весьма специфических проблем. Однако, можно рассмотреть предельные случаи водонасыщенной среды, различаемые по степени связности между твердой и жидкой фазами грунта.
Первым предельным случаем является среда "без связи", в которой жидкость свободно циркулирует между зернами твердой фазы (маловлажные пески, песчаники). Второй предельный случай ? "совершенная связь", характеризуется тем, что жидкость не может циркулировать в замкнутых порах (глины, известняки) и выдавливается из них при действии внутренних напряжений.
Критерием для оценки перехода к предельным случаям является значение безразмерной константы

где m ? пористость, rf и rs ? плотность жидкой и твердой фаз, A ? полуширина фундамента, KF
? коэффициент фильтрации, C2 ? скорость распространения поперечной волны, g ? ускорение свободного падения. Константа В в среде без связи стремится к нулю, а в среде с совершенной связью ? к бесконечности. При этом основными характеристиками, определяющими значение В, являются скорости распространения продольной и поперечной волн V1 и V2, а также коэффициент Пуассона.
Для среды без связи скорости распространения волн вычисляются по формулам

где l и m — параметры Ляме.
Для среды с совершенной связью

Здесь Ks и Kf — истинные модули сжимаемости твердой и жидкой фаз.
Расчеты для указанных предельных случаев выполняются как для упругой среды со следующими значениями определяющих упругих параметров:
- коэффициент Пуассона n = (1 - 2b2)/(2 - 2b2), где b = С2/С1;
- модуль упругости Е = 2m(1 + n).
Необходимо отметить, что константа В зависит от размера фундамента, и при одних и тех же грунтах использование той или иной расчетной модели будет также зависеть от полуширины фундамента А. Так, например, для водонасыщенного песка с характеристиками l = 0,23´109
Н/м2; m = 0,1´109 Н/м2; Ks = 3,6´1010
Н/м2; Kf = 1,92´109 Н/м2; m = 0,45; rs = 2,65´103
Н/м3; rf = 1,0´103
Н/м3; КФ = 10-2 м/с критериальная константа В = 0,52А. Следовательно, при малых размерах фундамента В Þ 0 (или, точнее, В << 1) и можно пользоваться моделью "среды без связи" с характеристиками n = 0,35 и Е = 2,7´108
Н/м2.
20.5. Использование абсолютно жестких вставок
При расчете стержневых систем часто возникает необходимость учесть эксцентричность стыковки элементов в узлах (рис. 20.14.а).
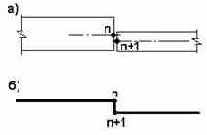
Рис. 20.14. Ступенчатый стык
Вставка между узлами n и n+1 стержня с очень большой, но конечной жесткостью, как это представляется интуитивно возможным, приводит к резкой потере точности вычислений за счет ухудшения числа обусловленности матрицы жесткостей [29]. Для обхода этой вычислительной трудности в комплексе SCAD предусматривается возможность использовать бесконечно жесткие вставки по концам стержневых элементов. Тогда расчетная схема имеет только один узел, занимающий произвольное положение на прямой между узлом n и узлом n+1, и к этому узлу концевые сечения соседних элементов присоединяются через жесткие вставки. Потеря точности в этом случае не наблюдается[1]. Проще всего можно поступить, если единственный узел N совместить с одним из узлов пары n, n+1, тогда абсолютно жесткая вставка появиться только у одного из элементов.
Платой за это упрощение является то, что внутренние усилия будут определены лишь на упругой части стержня.
Использование абсолютно жестких вставок особенно рекомендуется в тех случаях, когда рассматривается плита или оболочка, подкрепленная ребрами, эксцентрично расположенными по отношению к срединной поверхности. Если эти ребра моделируются стержневыми элементами, то учесть эксцентриситет можно лишь при использовании абсолютно жестких вставок.
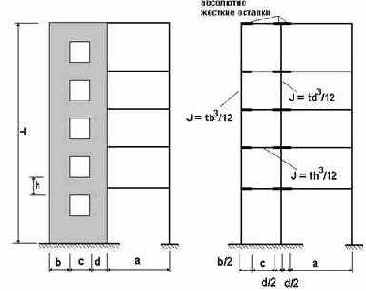
Рис. 20.15.
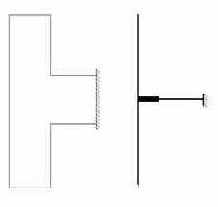
При расчете стержневых систем высота сечения обычно не превышает 1/8 ¸ 1/10 расстояния между узлами. Но встречаются конструкции, когда это отношение доходит до 1/5 или даже 1/3 (некоторые виды фундаментов под турбоагрегаты, диафрагмы зданий, гидротехнические сооружения и др.). В этом случае стержневая расчетная схема с точечными узлами, расположенными на пересечениях осей элементов, становится некорректной. Широко распространено предложение учитывать при этом реальные размеры "узлов", используя для этих целей стержневые элементы с бесконечно жесткими вставками. Пример такой схемы, построенный в соответствии с рекомендациями [32], представлен на рис. 20.15. Этот прием настолько давно используется, что расчеnчики практически никогда не задают вопрос о правомерности использования гипотезы недефомируемости "узла". Вместе с тем он далеко не лишен смысла, что видно из рассмотрения результатов расчета модельной задачи (рис.20.16)
 |
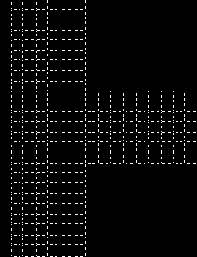 |
В ее стержневой модели горизонтальные перемещения отсутствуют, и вертикальный стержень не изгибается. Более детальная расчетная схема указывает на наличие горизонтальных перемещений, которые возникают вследствия стеснения деформаций сжатия по линии сопряжения АБ. Поскольку на противоположной стороне "стойки" этого стеснения нет, то возникает неравномерность распределения напряжений, эквивалентная изгибу.
20.6. Расчет на заданные перемещения
Необходимость расчета на заданные смещения возникает в практике проектирования чаще всего тогда, когда рассматриваемая система прикреплена к другой намного более мощной системе, которая не входит в расчтеную модель и играет роль "земли". Если упомянутая мощная система испытывает некоторые деформации, то для рассчитываемой конструкции следует учесть навязываемые смещения опорных узлов. Необходимо обязательно отметить, что могут задаваться лишь те перемещения узла, которые в отсутствие деформационного равны нулю (неподвижны), т.е. этот тип нагружения определяется перемещениями связей.
Для расчета на заданные смещения связей в SCAD предусмотрено использование нуль-элементов [17], схема простейшего элемента такого типа представлена на рис. 20.17. Он представляет собой комбинацию последовательно соединенных друг с другом пружин положительной жесткости С
и отрицательной жесткости -С. Поскольку для последовательно соединенных элементов податливости 1/С и 1/(-С) суммируются, то полученный элемент суммарной нулевой податливости по отношению к взаимному смещению его крайних узлов является абсолютно жесткой связью.
Если в качестве внешнего воздействия на систему необходимо приложить принудительное смещение пары внешних узлов на величину D, то достаточно приложить к внутреннему узлу нуль-элемента силу силу Р = СD и уравновесить ее в другом узле (см. рис. 20.17.б).
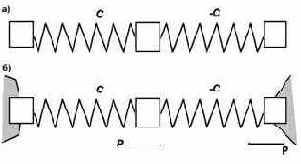
Рис. 20.17. Нуль-элемент
Все приведенные выше рассуждения остаются справедливыми при любом ненулевом значении параметра жесткости С, но исходя из соображений хорошей обусловленности матрицы жесткостей системы рекомендуется выбирать его не слишком отличающимся от жесткостных параметров близлежащих элементов.
20.7. Скрытые жесткости
Сочетание в одной расчетной схеме элементов (стержней), базирующихся на различных теориях, требует особо внимательного отношения расчетчика к формированию расчетной схемы конструкции. Комплексные механические модели подобного рода могут провоцировать получение некорректных результатов расчета.
В качестве иллюстрации высказанного положения рассмотрим следующую простую по своей постановке задачу. Пусть требуется произвести расчет однопролетной многоэтажной (20 этажей) рамы (так называемой “этажерки”), изображенной на рис. 20.18.
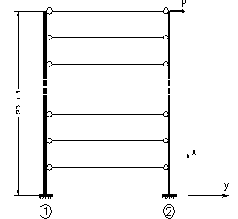
Рис. 20.18. Схема с двумя типами стержней
Пусть более мощная стойка рамы (стойка “1” на рис.20.18) имеет характеристики, в отношении которых расчетчик принимает решение о необходимости учета деформаций сдвига. Иначе говоря, для стойки “1” в расчетной схеме используется теория Тимошенко для изгибаемого стержня. Пусть далее в отношении стойки “2” принимается решение об использовании классической теории изгиба стержней, то есть теории Бернулли-Эйлера, основанной на гипотезе плоских сечений при пренебрежении деформаций сдвига. Что касается шарнирно присоединенных к стойкам ригелей, то будем считать их недеформируемыми в продольном направлении, то есть абсолютно жесткими на растяжение - сжатие.
Расчет, изображенной на рис. 20.18 рамы не представляет каких-либо затруднений и может быть выполнен по любой из имеющихся в распоряжении инженера-расчетчика программных систем, способных обрабатывать как стержни Тимошенко, так и классические стержни Бернулли-Эйлера. Возьмем для примера следующие (условные и заданные в условных единицах измерения) жесткостные характеристики, а именно положим:
EI1
= 3,5·109 , GF1 = 16,0·106 , EI2
= 3,5·107 .
Естественно ожидать, что основная часть нагрузки будет восприниматься более мощной стойкой, то есть стойкой “1”, так как ее изгибная жесткость EI1 на два порядка превышает аналогичную жесткость EI2 стойки “2”. Однако результаты выполненного расчета неожиданно (на первый взгляд) показывают, что значение поперечной силы в нижнем сечении стойки “1” равняется Q1(0) = 0,275Р, тогда как на стойку “2” передается вся оставшаяся часть нагрузки, то есть Q2(0) = 0,725P. Подобное распределение поперечных сил противоречит привычной инженерной интуиции, ожидающей как раз противоположного результата.
Для того чтобы понять причины происхождения этого эффекта, следует учесть, что за условием пренебрежения деформаций сдвига для стерженя Бернулли-Эйлера кроется предположение о его бесконечной жесткости на сдвиг, в то время как для стержня Тимошенко она имеет вполне определенную конечную величину. Именно эта скрытая бесконечная жесткость и определяет перераспределение усилий в системе.
20.8. Учет несовершенств системы
Расчет, выполняемый с помощью SCAD, основывается на использовании идеализированной расчетной модели, которая, вообще говоря, не учитывает возможные неидеальности. К сожалению, отечественные нормативные документы не уделяют этой проблеме должного внимания. Поэтому приведенные ниже рекомендации базируются на зарубежном опыте, который представлен в Еврокоде-3 (см. ENV 1993-1-1. Design of steel structures. - part 1 "General rules and rules for building").
Еврокод регламентирует некоторые элементы общего статического расчета несущей системы, допуская определение внутренних сил и моментов методами:
упругого расчета - для любых систем;
упруго-пластического или жестко-пластического расчета ? для систем с необходимым подкреплением против потери устойчивости.
Упругий расчет по недеформированной схеме допускается в тех случаях, когда приращения внутренних сил и моментов DR, возникающие за счет учета влияния перемещений системы под нагрузкой, не превышает 10% от величины R, полученной без учета этого влияния. В частности, для ортогональных многоэтажных рам расчет по недеформированной схеме возможен если
(d/h) £ 0,1(SH/SV),
где: d ? горизонтальное смещение верха рамы, h ? общая высота конструкции,
SH ? сумма горизонтальных реакций, SV ? общая вертикальная сила, действующая на раму.
Возможные несовершенства реальной системы могут привести к снижению уровня критической нагрузки (по сравнению с результатами расчета идеализированной системы). В связи с этим не рекомендуется применять конструкции, у которых коэффициент запаса по общей устойчивости меньше 1,25.
В отличие от СНиП, EUROCODE требует учета возможных начальных несовершенств и при выполнении общего статического расчета системы. В общем случае учету подлежат несовершенства системы в целом, несовершенства (неидеальность) узловых соединений и несовершенства элементов конструкции.
Для многоэтажных рам таким несовершенством является отклонение от вертикали
Y = kcksYo,
где: Yo ? допускаемый перекос колонны (например, Yo = 1/200);
kc = (0,5 + 1/nc)1/2, но kc £ 1;
ks = (0,2 + 1/ns)1/2, но ks £ 1;
ns ? число этажей;
nc ? общее число колонн, проходящих через все этажи, у которых нагрузка не ниже 50% от средней нагрузки на колонну.
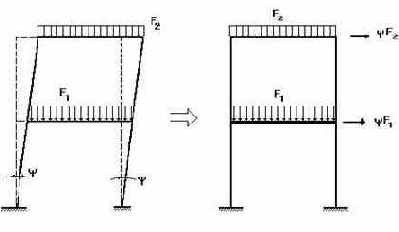
Допускается учитывать эти отклонения в виде эквивалентных горизонтальных сил по схеме рис.20.19. Такие силы могут действовать по всем возможным горизонтальным направлениям и необходимо выбрать неблагоприятные из них (например, для схемы по рис. 20.19, если ветер на раму действует слева направо, то неблагоприятным будет направление сил yF1
и yF2 ? тоже слева направо).
 |
|
Рис. 20.19. Эквивалентные силы для учета отклонений от вертикали |
 |
|
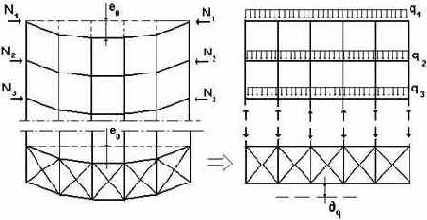
Рис. 20.20. Эквивалентные силы для связевых систем |
= (0,2 + 1/nr)1/2, но kr £ 1; nr - число подкрепляемых элементов.
Эквивалентная нагрузка на связевую систему
q = (SN/L)(kr + 500dq/L)/62,5,
где dq ? прогиб связевой системы (рис.20.20). В тех случаях, когда связевая система стабилизирует изгибаемые элементы, усилия N могут быть определены как
N = M/h,
где M ? максимальный изгибающий момент и h ? высота изгибаемого элемента.
Литература к главам 19 и 20
1. Блехман И.И., Мышкис А.Д., Пановко Я.Г. Механика и прикладная математика: Логика и особенности приложений математики. -– М.: Наука, 1983. –328 ñс.
2. Власов В.З., Леонтьев Н.Н. Балки, плиты, оболочки на упругом основании. —–
М.: Гос.изд. физ.-мат.лит., 1960.
3. Вовкушевский А.В., Шойхет Б.А. Расчет массивных гидротехнических сооружений с учетом раскрытия швов. —– М.: Энергия, 1981. – —136 с.
4. Джордж А., Лю Дж. Численное решение больших разреженных систем уравнений.-– ÌМ.: ÌèðМир, 1984.-–
333 ñс.
5. Динамический расчет зданий и сооружений (Справочник проектировщика) /Под ред. Б.Г.Коренева и И.М.Рабиновича. -– М.: Стройиздат, 1984.- – 303с.
6. Динамический расчет сооружений на специальные воздействия (Справочник проектировщика)
/Под ред. Б.Г.Коренева и И.М.Рабиновича. -– М.: Стройиздат, 1981. -– 215с.
7. Доннелл Л.Г. Балки, пластины и оболочки. М.: Гл. ред. ф.-м. наук, 1982. – 568 ñс.
8. Евзеров И.Д. Оценки погрешности несовместных конечных элементов плиты. Деп. в УкрНИИНТИ, №1467. –— Киев, 1979. –—
9 с.
9. Елсукова К.П., Сливкер В.И. Некоторые особенности МКЭ при расчете конструкций на упругом основании.
–— В кн. Метод конечных элементов и строительная механика. Труды ЛПИБ №349. —– с.69-80.
10. Зенкевич О. Метод конечных элементов в технике. –— М.: Мир, 1975. —– 542 c.
11. Зенкевич О., Морган К. Конечные элементы и аппроксимации. МÌ.: ÌèðМир, 1986. –
318 ñс.
12. Зенкевич О.К., Айронс Б.М., Скотт Ф.К., Кемпбелл Дж. С. Анализ трехмерного напряженного состояния. —– В кн.: Расчет упругих конструкций с использованием ЭВМ. Том 1. —–
Л.: Судостроение, 1974, с. 293-305.
13. Карпиловский В.С. Методы конструирования конечных элементов. Деп. в УкрНИИНТИ, №3153.— –
Киев, 1980.
–— 20 с.
14. Метод суперэлементов в расчете инженерных сооружений. /В.А.Постнов, С.А.Дмитриев, Б.К.Емышев, А.А.Родионов. –- Л.: Судостроение, 1989. -– 288с.
15. Методы расчета стержневых систем, пластин и оболочек с использованием ЭВМ. ÷àñòüЧасть
11. / Под ред. Смимрнова А.Ф./ М.: Стройиздат, 1976. – 248 с.
16. Пастернак П.Л. Основы нового метода расчета фундаментов на упругом основании при помощи двух коэффициентов постели. – М. – Л.: Гос. изд. лит. по строительству и архитектуре, 1954.
17. Перельмутер А.В., Сливкер В.И. О реализации сложных кинематических условий при расчете дискретных систем методом перемещений. – В кн.: Метод конечных элементов и строительная механика. Труды ЛПИ N 369. Л 1979. С.26-39.
18. Пискунов В.Г., Карпиловский В.С. и др. Расчет кpановыx констpукций методом конечныx элементов. М.: Машиностроение, 1991. – 240 с.
19. Пискунов В.Г., Федоренко Ю.М. Динамический метод контроля состояния слоистых плит на упругом основании, Архитектура и строительство Белоруси, №5-6, 1994, с.19-22
20. Работнов Ю.Н. Механика деформируемого твердого тела. М.: Гл. ред. ф.-м. наук,1988. – 712 с.
21. Ржаницын А.Р. Устойчивость равновесия упругих систем. М.: Гостехстройиздат, 1955. – 475 с.
22. Сеймов В.М., Трофимчук А.Н., Савицкий О.А. Колебания и волны в слоистых средах. – Киев: Наукова думка, 1990.
23. Смирнов А.Ф., Александров А.В., и др. Строительная механика. Стержневые системы. М.: Стройиздат, 1981. – 512 с.
24. СНиП II-7-81. Строительство в сейсмических районах / Госстрой СССР. – М.:Стройиздат, 1982. – 48 с.
25. Стрелец-Стрелецкий Е.Б. Расчетные сочетания напряжений для конструкций типа балки-стенки и плиты. Строительная механика и расчет сооружений. 1986. N3.
26. Стренг Г., Фикс Дж. Теория метода конечных элементов. – М.: Мир, 1977. – 350 с.
27. Сьярле Ф. Метод конечных элементов для эллиптических задач. М.: Мир, 1980. – 512 с.
28. Феодосьев В.И. Десять лекций-бесед по сопротивлению материалов. – М.: Наука, 1969.
29. Чу К.-С. Определенный вид плохо обусловленной матрицы жесткостей, Ракетная техника и космонавтика, 1973, №1, с.125-127.
30. Sabahi D., Rose T. Special Applications of Global-Local Analysis, MSC/NASTRAN 1992 World Users` Conference Proceedings.
31. Schiermeier J.E., Housner J.M., Ranson J.B., Aminpour M.A., Stroud W.J. The Application of Interface Element to Dissimilar Meshes in Global/Local Analysis, MSC 1996 World Users` Conference Proceedings
32. Городецкий А.С., Евзеров И.Д., Стрелец-Стрелецкий Е.Б., Боговис В.Е., Гензерский Ю.В., Городецкий Д.А. Метод конечных элементов: теория и численная реализация. Программный комплекс "Лира-Windows". – К.: ФАКТ, 1997.
